team pulse ♥️

Objective

The purpose of this milestone was to improve our robot’s right-hand wall following algorithm to some sort of an algorithm that allows it to more effciently and quickly explore a maze. By the completion of this milestone, our robot explored a maze by prioriting intersections that it hadn’t visited before, and visiting those intersections. After completing this milestone, we added an even better algorithm for the final competition, which you can read more about here.

Design

After deciding that we wanted to implement a path planning algorithm for our robot, we broke down the creation of the algorithm into intermediate steps to ensure that our robot would have some sort of working, optimized algorithm in the following order:

1) Turn-by-turn with wall avoidance

2) Turn-by-turn with wall avoidance and priority on unvisited neighboring locations

3) Priority on unvisited neighbors, wall avoidance, and path planning

Each of our newer algorithms built off of the previous.

Implementation

We broke down the creation of our algorithm(s) into two steps: 1) writing an improved maze exploration algorithm and 2) testing the algorithm on our robot and updating the maze map GUI on the base station.

Note: our latest software works such that our robot can only check for walls and make decisions about movement at an intersection. All of our maze-solving algorithms were written with this understanding.

Maze Exploration

1) First Algorithm: Turn-By-Turn with Wall Avoidance

Similar to our right-hand wall following algorithm (from Lab 3) is a maze traversal with wall avoidance. With this algorithm, the robot moves forward at every intersection until it sees a wall in front of it. It then checks for a wall to the left of itself (turns left if there is none), then to the right of itself (turns right if there is none). If it detects a wall in front of, to the left of, and to the right of itself, the robot turns around 180 degrees.

Pros: A start to our second maze algorithm. Cons: Can get stuck in many maze configurations–i.e. doesn’t map the entire maze.

2) Second Algorithm: Turn-By-Turn with Wall Avoidance and Priority on Unvisited Neighbors

This algorithm uses our previous one, but it puts proritizes unvisited neighboring intersections. That is, our robot is able to analyze the walls to the front and side of itself, and travel first to intersections that haven’t been previously visited.

To check whether neighboring intersections have been visited or not, we implemented a simple 2D array of ints as our data structure, and kept track of data in the following way:

// ==== Maze Array Explanation ====
//
//   Array stores each integer value 
//   as follows:
//
//                       N E S W
//   [ 0 0 0 |    0    | 0 0 0 0 ] 
//             Visited    Walls
// ================================
/*
xpos = 0, ypos = 0 is the top left hand corner of the maze. The robot assumes it starts at (0, 0). X increases
left to right and Y increases top to bottom. When we visit an intersection, we set the visited bit to 1. We set wall bits as appropriate.*/

Our logic is fairly simple. When at an intersection, we first check for walls using bits 0 through 3 in our maze[][] array. We then check whether the adjacent squares have been visited by checking the visited bit (bit 4). We achieve such by bit shifting and bitwise operations:

//Wall values assignment
byte WP, L, B, R;
  L = (wallvalleft > WALLTHRESHOLD) ? B01 : 0;
  B = (wallval > WALLTHRESHOLD) ? B01 : 0;
  R = (wallvalright > WALLTHRESHOLD + 30) ? B01 : 0;
  WP = (L<<2) | (B<<1) | R ;
  
 //Assign walls for maze update and transmission
 switch(orientation % 4){
        case 0:
          walls = (B << 3) | (R << 2) | L ; // 1 1 0 1
          break;
        case 1:
          walls = (L << 3) | (B << 2) | (R << 1) ; // 1 1 1 0
          break;
        case 2:
          walls = (L << 2) | (B << 1) | R ; // 0 1 1 1
          break;
        case 3:
          walls = (R << 3) | (L << 1) | B ; // 1 0 1 1
          break;
      }
      
  //Check whether adjacent squares are visited
  switch(orientation % 4){
        case 0:
          L = (xpos > 0) ? maze[xpos - 1][ypos] & (1 << 4) : 0;
          B = (ypos > 0) ? maze[xpos][ypos - 1] & (1 << 4) : 0;
          R = (xpos < 8) ? maze[xpos + 1][ypos] & (1 << 4) : 0;
          break;
        case 1:
          L = (ypos > 0) ? maze[xpos][ypos - 1] & (1 << 4) : 0;
          B = (xpos < 8) ? maze[xpos + 1][ypos] & (1 << 4) : 0;
          R = (ypos < 8) ? maze[xpos][ypos + 1] & (1 << 4) : 0;
          break;
        case 2:
          L = (xpos < 8) ? maze[xpos + 1][ypos] & (1 << 4) : 0;
          B = (ypos < 8) ? maze[xpos][ypos + 1] & (1 << 4) : 0;
          R = (xpos > 0) ? maze[xpos - 1][ypos] & (1 << 4) : 0;
          break;
        case 3:
          L = (ypos < 8) ? maze[xpos][ypos + 1] & (1 << 4) : 0;
          B = (xpos > 0) ? maze[xpos - 1][ypos] & (1 << 4) : 0;
          R = (ypos > 0) ? maze[xpos][ypos - 1] & (1 << 4) : 0;
          break;
      }

We then use the L, B, and R variables to have our robot go in the direction of the neighbor it hasn’t visited, or by default prioritize going forwards, left (second priority), right (third priority), or turn around 180 degrees (last priority).

Example:

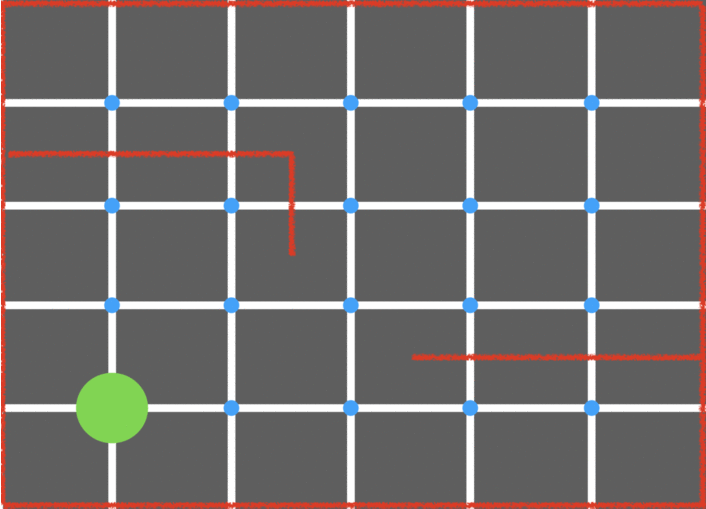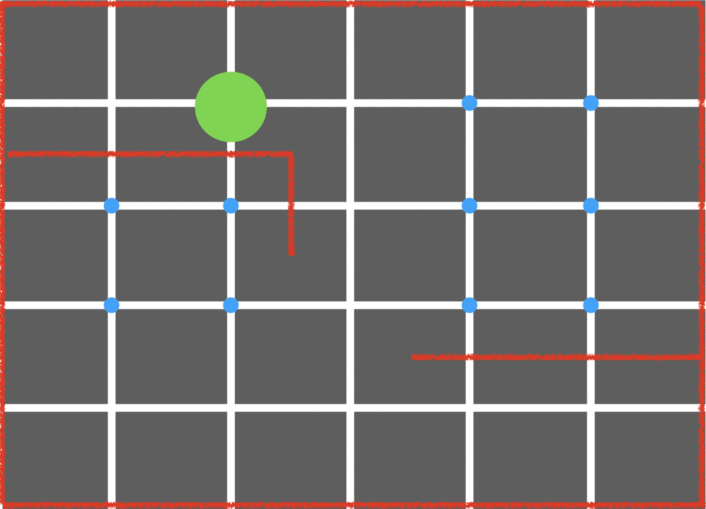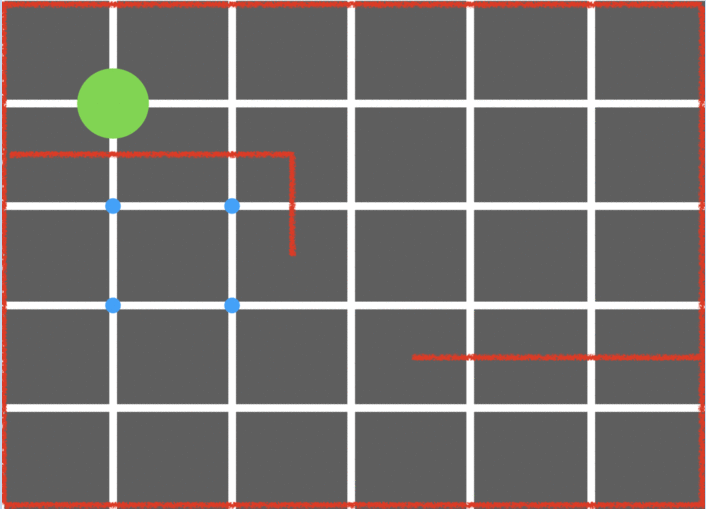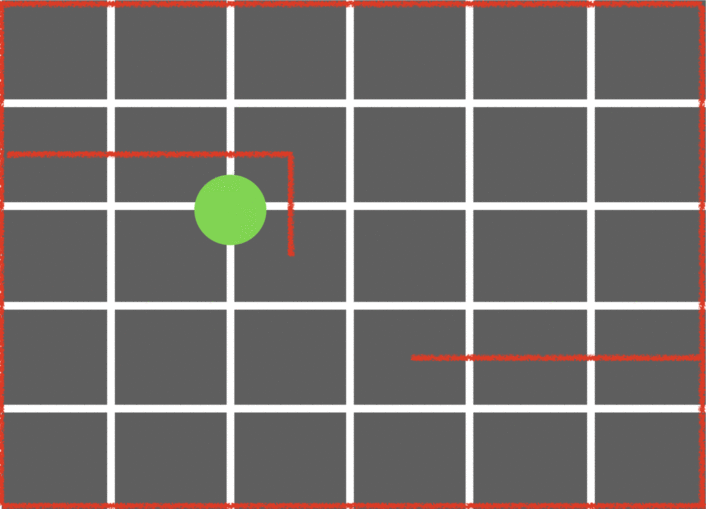
Pros: Allows the robot to explore more of the maze, data structure that doesn’t use up too much memory, fairly easy implementation. Cons: Not extremely efficient for solving an entire maze.

3) Third Algorithm: Priority on Unvisited Neighbors, Wall Avoidance, and Path Planning

After we completed this milestone, we built upon our second algorithm by adding searching and path planning. You can read about it in our final robot design here.

Testing on Robot and Updating the GUI

We tested our algorithms on various maze sizes and wall orientations:

6x4 Maze:

3x5 Maze:

Our robot was also able to transmit maze information to our GUI: